【导读】2020安徽农商行社会招聘公告暂未发布，笔试时间为公告发布后的一个月之后。力锐教育为大家整理了2020安徽农商行校园招聘公告|职位表|报名时间|报名入口|考试时间备考专题，考生可提前收藏专题页面，我们在公告发布第一时间同步更新，更多关于2020安徽农商行招聘备考信息可关注力锐教育。

比较构造的定义：对同一事物进行两种不同方案的分配，比较两种方案的差别，找出其中的等量关系再列出方程，这就是比较构造法。它的优势在于直接比较差异，列出最简形式的方程，来节约化简方程的时间。

一、比较构造法列普通方程;

我们先来看一道较为简单的题目：

【例题1】将一些糖果分给小朋友们，如果每小朋友分12颗，则多出3颗糖果，如果每个小朋友分14颗，则又缺5颗糖果，共有多少个小朋友?

A.4 B.5 C.6 D.7

【中公解析】方法一：拿到这道题，我们明显发现无论怎么分配，糖果总数是不变的，所以可以根据这个等量关系列方程，我们可以设小朋友的人数偎x人，可以列出等量方程：12x+3=14x-5，化简方程，解得x=4，选A.

方法二：让我们来看一看怎么用比较构造法的思维去解题，比较一下我们两种分配方式的差异，我们发现：每个小朋友12颗糖果比每个小朋友14颗糖果的剩余的数量多3+5=8个，所以每个小朋友分12颗糖果的总数比每个小朋友分14颗糖果的总数要少8个，如下表所示：

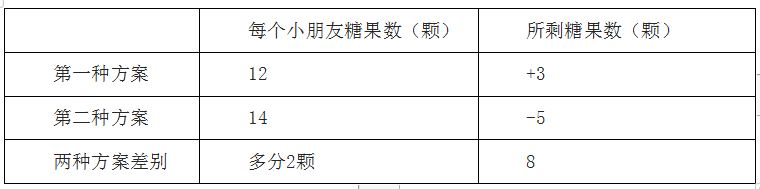
也就是说如果多8颗糖果，每个小朋友能多2颗糖，那显然有8&pide;2=4个小朋友，选A。

【例题2】用绳子测井深，把绳子折成二折去测量井深，井口外余3米;再把绳子折成三折去测量井深，井口外余1米，求井有多深?

A.4 B.5 C.7 D.3

安徽农商行招聘网解析：方法一：常规方法可设井深为x，然后利用绳子长度不变找到等量关系，得到方程：2(x+3)=3(x+1)，化简解得x=3，则井深为3米，选D。

方法二：用比较构造法思考，类比例题1，我们能列出下表：

通过对比我们发现第二次测量时多了一折，即多了一倍井深而绳子少了3米，即为井深，故选D。

通过两个例题的常规方程列法与比较构造法进行比较，我们能体会到比较构造法在形式上更为简易。

二、比较构造法列不定方程;

其实我们比较构造法不止能解普通方程，还可以解不定方程，我们来看一道例题：

【例题3】某干旱地区为鼓励居民节约用水，对自来水用户按分段计费方式收取水费：在标准以内，每立方米的水费为1.2元，超过标准线的部分每立方米多交0.3元;如果标准用水量为5吨，那么张家比李家多交水费5.4元，若水费标准和两家用水量都是正整数，那么张家比李家多用几吨水?

A.2 B.3 C.4 D.5

安徽农商行招聘网解析：设张家用水x吨，李家用水y吨，则有三种可能性：

1.若两家用水都在标准用水量以内，方程为：1.2x-1.2y=5.4，显然无正整数解，排除;

2.若两家用水都在标准用水量以外，方程为：(1.2+0.3)x-(1.2+0.3)y=5.4，显然也无正整数解，因此排除;

3.张家用水超过标准用水量，李家用水低于标准用水量。

方法一：我们还是用常规解题思维常规方法可以得到：张家总水费为1.2×5+(x-5)·(1.2+0.3)，李家水费为1.2y，则方程为：

1.2×5+(x-5)·(1.2+0.3)-1.2y=5.4，化简得：1.5x-1.2y=6.9，利用解不定方程的同余特性解方法得x=7，y=3，张家比李家多：x-y=4吨，选C。

方法二：设张家比标准用水量多x吨，那么张家水费比标准水费多(1.2+0.3)x=1.5x，设李家比标准用水量少y吨，那么李家水费比标准水费少1.2y，如下表：

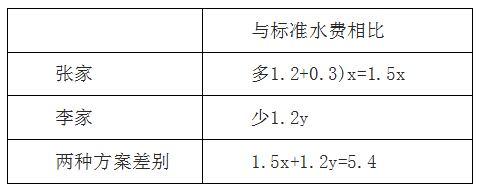
对于方程方程：1.5x+1.2y=5.4，利用同余特性解得：x=2，y=2。则张家用水5+2=7吨，李家用水5-2=3吨，张家比李家多7-3=4吨，选C。

安徽农商行考试交流群：529852728

咨询QQ：1927004227

银行/安徽农商行考试复习综合教材

力锐教育官方微信公众号